top of page
PBI Teaching Experience
pbi-teaching-experience
Gainesville High School | Geometry Honors | Geometry Cambridge | 9th - 11th Grade
Overview: This fall (2023), I had the opportunity to teach Geometry under the mentorship of Mrs. Crews at Gainesville High School. Throughout this experience, I learned an immense amount of knowledge regarding adaptivity, flexibility, and self-reflection as an educator. This includes observing the needs of students, implementing elements of wait-time to foster appropriate pacing for lessons. Being aware of misconceptions and constantly interacting with each student, walking throughout an entire classroom. And using mistakes as a form of learning, utilizing such as assets toward future growth. As an intern, I greatly enjoyed interacting with a phenomenal group of students who taught me a lot about education, and how I can evolve my methodologies to facilitate a positive classroom experience.
Topics Covered:
-Parallel and Perpendicular Lines (3.1 - 3.5)
-Transformations (4.1 - 4.6)
-Congruent Triangles (5.1 - 5.8)
Lessons Taught (link provided):
-Dilations (4.5)
-Congruent Transformations (4.4)
-Triangle Review (5.1 - 5.4: Angles, Congruent Polygons, Equilateral, Isosceles)
-Congruent Triangles Jeopardy (5.1 - 5.6)
-Congruent Triangle Proofs (5.1 - 5.6: SAS, SSS, ASA, AAS, HL)
Breakdown of Lessons:
Congruent Triangle Jeopardy (5.1 - 5.6)
Summary: A comprehensive review of angle pair relationships, five triangle congruency theories, and proofs.
Student Artifacts:
[1] The following is a $500 question from the "Proofs" category of Jeopardy. As noted in the student's answer, various definitions and theorems are utilized to arrive at a finalized congruency statement, in this case 'AAS.' The purpose of this question is to resemble the difficulty of those on the Geometry EOC, often containing various drag-response answers for two-column proofs. This student and their group showcased the correct answer on a whiteboard to earn credit and receive feedback.
[2] The following is a $500 question from the "Random" category of Jeopardy. The intention of this question is to distinguish the difference between a theorem and a converse, specifically for Base Angles. The answer to this question was displayed on a whiteboard to earn credit.
[3] The following is a $300 question from the "Random" category of Jeopardy. This question is meant to reiterate the Exterior Angle Theorem, indicating the summation of two interior angles is congruent to the measure of an exterior angle. This student and their team showcased their correct answer on the board and stated their step-by-step process of solving the problem.
Summary: A comprehensive review of the five triangle congruency theorems: SAS, SSS, ASA, AAS, HL
Student Artifacts:
[4] The following is an example of a 'AAS' Congruence theorem proof in a two-column format. Evidently, this student initially thought that it was an HL Congruence Theorem proof simply based on the presence of right angles. But, this is not true since we don't have both a congruent a leg and hypotenuse for both triangles. This example was included to reveal a common student misconception; we must prove a triangle in the case of 'AAS,' but 'HL' is assumed just because of marked right angles. Correspondingly, I clarified the misunderstanding by solving it on the whiteboard.
[5] The following is an example of a correct 'HL' congruence theorem proof. As noted, the student understands how a midpoint implies two congruent segments EG and HG. Therefore, there are two congruent sides (hypotenuse and leg) and a congruent pair of right angles. This example was included to challenge students to prove 'HL' with various definitions they've learned in previous units.
[6] The following is an example of a incorrect pair of statements and reasons for proving 'SAS' congruence theorem. The student appears to write the order of triangles 'PQT' and 'RST' incorrectly, and uses the reflexive property in an inapplicable circumstance. The student was corrected individually once demonstrating their answer via whiteboard. This illustrates how proofs can be a difficult topic to master and are inherently important for the EOC.
Congruent Triangle Proofs (5.2, 5.4 - 5.6)



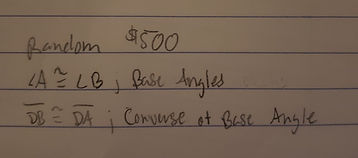








Formative Assessments:
Congruent Triangle Jeopardy (5.1 - 5.6)
Think-Pair-Share: for our game of Jeopardy, students were arranged into groups of 4 - 5 to solve problems collaboratively. Specifically, per each prompt assigned to the students, they would initially brainstorm independently, then combine their rationale to generate a step-by-step solution on their whiteboard for presentation. As a cohesive group, they were required to compare their thinking methodologies and utilize such to create a final justification toward their answer in order to earn points. This formative assessment facilitated a quick form of evaluation per each group of students, allowing me to quickly correct any misconceptions immediately after a question. Moreover, any form of mistakes made by the students were resolved in a low-stakes environment where they weren't penalized academically. The game-centric atmosphere facilitated a team-orientated, dynamic, social lesson where students' levels of understanding could be easily recognized and refined from the perspective of an educator.
Whiteboarding: to corroborate our game of jeopardy, students were required to devise a justified solution to each question via whiteboard for presentation. Each group of 4 - 5 students possessed a whiteboard and rotated a 'presenter' per question. Embedding this formative strategy enhanced the quick feedback I could propose to students with any misconceptions immediately after a question. Moreover, if multiple groups of students got the same question wrong, that would indicate more time to be allocated toward reviewing the answer. Thus, for many proof-based questions, we would spend greater intervals of time reviewing on the main board based on the majority of answers being partially correct.
Wait Time Variations: for our comprehensive review of the five congruent triangle theorems, we followed a pattern - group example, independent examples, review, and repeat. When reviewing the answer to each congruent triangle proof, students' were asked to provide answers piece-by-piece for the statement/reason responses. Per each problem, various questions asked included: "What information are we given in this problem?" "What is the difference between an included angle and a non-included side?" "In what specific circumstance can we use the HL theorem? Isn't HL an example of 'SSA' and if so, why can we use it?" These types of questions were corroborated with approximately 3 - 7 seconds of wait-time for multiple reasons: facilitating a hortatory environment where each student has an equal opportunity to respond; gauging students' of understanding based on the lack or abundance of participation; nourishing critical thinking toward "why" an answer is correct as opposed to just being right or wrong. Implementing wait-time allowed me to pace a lesson appropriately to the needs of students, and understand which topics needed greater accommodation in comparison to others. Moreover, it helps defer away from a lecture-based classroom, encouraging students to learn through participation, and not fear being "correct" or "incorrect." For instance, for a particular series of proof question, the same student was attempting to answer the question repeatedly despite implementing wait-time. Thus, for the following question, I asked for an answer from a particular region of the room (back-left corner), and was greeted with an attempt from other students. Followingly, they began to participate more for the rest of the period.
Congruent Triangle Proofs (5.2, 5.4 - 5.6)
pbi-unit
PBI Unit: Geometry
Symmetry in Logos: Congruent Triangles!
Target Audience: High-school Geometry classes from 9th - 10th grade; aimed for Honors and Cambridge levels as an individual project.
Driving Question: We need you to create an engaging logo for a Gainesville organization offering free math tutoring for students within secondary education! How can the principles of congruent triangles and symmetry help you design a powerful geometric logo to reach our community? Why “eye-ball” your drawings when you can use math to guarantee precise and balanced visual aesthetics?
Project Description: Students will explore how triangles can be used to construct symmetric logos. By identifying four kinds of triangles - scalene, isosceles, equilateral, right - their pre-established conditions - side lengths, angle relationships - and corresponding lines of symmetry for each, we will gradually develop ½ of an original design using pairs of adjacent triangles. We will then reflect their designs across an axis to generate a full image and proving congruence of triangle pairs using at least all 5 triangle congruence theorems, Ultimately, students will deconstruct polygons within their design into triangle pairs to classify, label, and prove congruency based on side lengths and angle relationships.
Relevant Standards: Standards pertain to chapters focusing on Congruent Triangles and Applications of Congruent Triangles, specifically Chapter 5 of the Big Ideas Math textbook:
-
MA.912.GR.1.2: Prove triangle congruence or similarity using Side-Side-Side, Side-Angle-Side, Angle-Side-Angle, Angle-Angle-Side, Angle-Angle and Hypotenuse-Leg.
-
MA.912.GR.1.6: Solve mathematical and real-world problems involving congruence or similarity in two-dimensional figures.
-
MA.912.GR.3.2: Given a mathematical context, use coordinate geometry to classify or justify definitions, properties and theorems involving circles, triangles or quadrilaterals.
Learning Objectives: The following learning objectives cater to topics on congruent triangle theorems, lines of symmetry, and angle pair relationships.
-
Understand congruent triangles - classify by sides and angles.
-
Find interior and exterior angle measures of triangles.
-
Prove and use theorems about isosceles triangles. Prove and use theorems about equilateral triangles.
-
Use congruent triangles to solve real-life problems.
-
Place figures in a coordinate plane.
-
Use the SAS, SSS, ASA, AAS, and HL congruence theorems.
Project Presentation: students will combine their artifacts into a poster to represent the evolution in their design. This poster will include the following:
-
A print of each individual triangle and marked lines of symmetry
-
A printed final geometric design
-
Breakdown of design by…
-
Segment Lengths (distance)
-
Angle Measurements
-
Markings for Congruency
-
Presence of at least all 5 Triangle Proofs
-
Technology Incorporation: students will design their logos using the following online website: https://virtual-graph-paper.com/. Such allows a user to place vertex points on a grid-like plane and connect corresponding coordinates to generate segments. Moreover, it allows a user to measure the distance and angles between all their designed segments which will be used to prove the types of triangle presented: isosceles, right, and equilateral. For instance, if a student desires to prove that they have designed an equilateral triangle, they must utilize their vertex points to calculate the distance of each segment. This application also allows students to modify the fill and stroke color of their triangles to meet their personal preference in design.
Relative Timeline: The following is a timeline for the completion of this PBI unit: 50-minute class period per lesson spanning 5 cumulative class days.
Day
1
Task
Introduction: Real-Life Artwork with Triangles
Overview
Present logos and geometric patterns. Gauge student observations on congruent triangles, symmetry, and angle pair relationships with “prior-learning” formative assessment questions.
Assign students to brainstorm logo ideas for their math tutoring service based on community needs
Example Logos:

Day
2
Task
Activity: Evaluating Lines of Symmetry
Overview
Showcase examples of lines of symmetry:
-scalene (0 lines)
-isosceles (at least 1 line)
-equilateral (3 lines)
-right (0 or 1 line)
Assign students to create a digital example of each triangle and draw lines of symmetry. They will explain “why” their triangle is of the correct type by explaining relevant information on their side lengths and angles. Students will use the following online website: https://virtual-graph-paper.com/
Student Products: students will generate one of each kind - scalene, isosceles, equilateral, and right triangles - as long as they satisfy their respective conditions. This means justifying the validity of each triangle through the distance formula, vertex points, and appropriate calculations to showcase marked segment lengths and angle measurements. Examples include the following:

Day
3
Task
Activity: Combining Symmetrical Triangles
Overview
Students will build off of their previous triangles by building a simplistic geometric pattern using such. They must generate a combination of at least three types of triangles - isosceles, right, and equilateral - to form a pattern. Additionally, they must prove each triangle is of the correct type by measuring the distance and angles between all their segments.
Student Products: Students may generate a pattern such as the following: Green represents an equilateral triangle. Blue represents a right triangle. White represents an isosceles triangle. Note that students can measure segment lengths and angles within the program, and correspondingly calculate distance. They must prove that the pattern they've created possesses at least one of each triangle be labeling the lengths and angles on each.

Day
4 - 5
Task
Activity: Reflecting a Pattern and Proving Congruency
Overview
Students will build off of their previous triangles by building a simplistic geometric pattern using such. They must generate a combination of at least three types of triangles - isosceles, right, and equilateral - to form a pattern. Additionally, they must prove each triangle is of the correct type by measuring the distance and angles between all their segments. Assign poster assignment for weekend!
Student Products: Students will begin to generate their logo by reflecting across the x or y-axis of a coordinate plane. With their adjacent pairs of triangles, they must prove congruency using at least one of each congruency theorem. For instance, in the example below: triangles 'CDF' and 'FEC' could be congruent within polygon 'CDEF' through either SSS, SAS, or even AAS. There are multiple options for a student to choose as long as they provide a two-column proof for each.

Day
6
Task
Share Project Presentation and Reflection
Overview
Students will demonstrate their final logo design for their math tutoring service through their poster; students will evaluate each other's patterns by answering a series of reflective questions
Rubric:



Contextual Relevance: The unit is designed around the context of designing logos for a community organization that offers free math tutoring services in Gainesville, FL. This context is likely to resonate with students as it connects the mathematical concepts to a real-world scenario that directly impacts their community. By addressing the specific needs of the community, students can see the practical applications of their mathematical skills into generating an image the resonates with service.
Student Engagement: The unit addresses potential variations in students' interests by allowing them to choose their own geometric design (colors, segment lengths, patterns) as long as the appropriate conditions are satisfied. By connecting students with a community organization, the designs of the logos for a math tutoring service contributes to a higher sense of stakes and importance for their choice of triangles; they must think before randomly placing triangles as it will impact the appearance and relationship amongst triangles in their final logo.
bottom of page